scikit-learn (sklearn)操作手册
卢圣华 2025年3月21日
本手册面向人工智能基础(B)课程的学生,旨在通过实践操作巩固机器学习理论知识。我们将使用 Python (基于 scikit-learn 库)实现常见的五种算法,包括:线性回归与逻辑回归、决策树、支持向量机、朴素贝叶斯和聚类。手册采用循序渐进的方式,每个模块提供贴近经济、金融、管理等领域的应用场景,详细的代码实现(包含充分注释),以及结果分析与拓展讨论。
在开始之前,请确保已安装必要的Python库,例如 numpy、pandas、scikit-learn 和 matplotlib。读者应具备基础的Python编程能力,会使用Jupyter Notebook或类似环境运行代码。
相关数据和代码,请点击以下链接进行下载,然后在本地Python环境或在MO平台运行。
这是一个机器学习实践课程的数据集集合,包含了以下数据集:
- 线性回归数据集:
sales_train.csv和sales_test.csv
- 包含广告预算和销售额数据
- 用于预测广告预算与销售额之间的线性关系
- 逻辑回归数据集:
credit_default_train.csv和credit_default_test.csv
- 包含信用评分和是否违约数据
- 用于预测客户是否会违约
- 决策树数据集:
user_purchase_data.csv
- 包含用户年龄、收入、是否学生、信用等级和是否购买的分类特征
- 用于预测用户是否会购买产品
- 支持向量机数据集:
customer_churn_data.csv
- 包含月使用时长、满意度评分和是否流失数据
- 用于预测客户是否会流失
- 朴素贝叶斯数据集:
spam_sms_data.csv
- 包含短信内容和标签(ham或spam)
- 用于文本分类,预测短信是否为垃圾短信
- 聚类数据集:
customer_segmentation_data.csv
- 包含客户收入和消费数据
- 用于客户分群分析
此外,还有一个 SimSun.ttf 字体文件用于支持中文显示,以及 sklearn_practice.ipynb 实践指南。
目录:
各部分结构大致如下:
- 背景与任务 – 介绍实际问题场景和学习目标;
- 数据准备 – 根据场景读取相关数据;
- 模型训练 – 使用
sklearn训练模型;
- 预测与评估 – 对模型进行预测及性能评估,包括适当的指标(准确率、均方误差、F1等)和可视化结果;
- 参数调整 – 简要说明关键参数的调整方法;
- 拓展讨论 – 扩展应用场景、算法优劣和改进方向等。读者可以按照每个步骤自行运行代码、观察结果,以获得直观的理解。
线性回归与逻辑回归
背景与任务: 回归算法用于预测连续数值,例如预测企业销售额、房价等;逻辑回归用于二分类问题,例如信用违约预测(借款人是否违约)、客户流失预测等。在经济管理领域,经常需要既能预测数值指标(如销售额、利润),又能判断类别结果(如客户是否流失)。本节通过两个示例场景演示这两种算法的实操:
- 线性回归示例: 根据广告投入预测产品销售额(连续值预测)。
- 逻辑回归示例: 根据信用评分预测客户是否违约(二元分类)。
我们将分别准备模拟数据,训练模型并评估性能,帮助理解回归与分类的区别和实现流程。
线性回归示例:销售额预测
场景背景: 假设我们在一家零售公司担任数据分析师,公司想根据广告投放预算来预测产品的销售额。经验表明,广告投入与销售额存在一定的线性相关关系。在这个示例中,我们的目标是学习如何使用线性回归模型,根据投入的广告费用预测相应的产品销售额。
我们将模拟一组数据:每条数据包含"广告预算"(自变量)和"销售额"(目标变量)。广告预算以万元计,销售额以单位数量计。通过该示例,我们希望掌握:
- 使用
sklearn.linear_model.LinearRegression建立线性回归模型;
- 模拟生成线性相关的数据集;
- 训练模型并获取回归系数;
- 使用模型对新数据进行销售额预测,评估预测的准确性(例如使用均方误差MSE和决定系数R²指标);
- 绘制回归拟合直线,直观展示模型效果。
数据读取
首先,我们来读取并查看数据
import pandas as pd
import numpy as np
# 读取训练集和测试集
df_train = pd.read_csv('sales_train.csv')
df_test = pd.read_csv('sales_test.csv')
# 恢复变量
X_train = df_train['广告预算'].values.reshape(-1, 1)
y_train = df_train['销售额'].values
X_test = df_test['广告预算'].values.reshape(-1, 1)
y_test = df_test['销售额'].values
# 查看前5条数据
print("训练集前5条数据:")
print(df_train.head())
print("\n测试集前5条数据:")
print(df_test.head())可以看到
训练集前5条数据:
广告预算 销售额
0 83.244264 439.452100
1 15.601864 93.224100
2 9.767211 75.845983
3 60.111501 333.993689
4 59.865848 326.318205
测试集前5条数据:
广告预算 销售额
0 21.233911 142.286318
1 44.015249 230.200558
2 60.754485 337.386382
3 66.252228 356.243572
4 52.475643 289.286092模型训练
接下来,我们使用LinearRegression建立线性回归模型,并在训练集上训练模型(拟合参数)。训练完成后,可以输出模型学到的回归系数(权重)和截距,用于解释模型。
from sklearn.linear_model import LinearRegression
# 2. 初始化线性回归模型并在训练集上训练
model_lr = LinearRegression() # 创建LinearRegression模型实例
model_lr.fit(X_train, y_train) # 拟合模型参数
# 输出模型的参数
coef = model_lr.coef_[0] # 回归系数(由于只有一个特征,可以取coef_[0])
intercept = model_lr.intercept_ # 截距
print(f"学到的回归系数β: {coef:.2f}")
print(f"学到的截距α: {intercept:.2f}")
训练过程中,模型会自动找到使预测值与训练集真实值误差最小的线性函数。打印结果例如:
学到的回归系数β: 4.97
学到的截距α: 31.24
可以看到,模型学到的系数约为4.97,截距约为31.24,与我们设定的真实值5和30非常接近。说明模型成功学到了广告预算与销售额的线性关系。
预测与评估
现在,我们使用训练好的模型对测试集的数据进行销售额预测,并评估模型的性能。我们将计算常用的回归指标:均方误差(MSE)和决定系数(R²)。MSE反映预测值与真实值的平均平方误差,越小越好;R²取值0~1,越接近1表示模型解释变量波动的能力越强。
from sklearn.metrics import mean_squared_error, r2_score
# 3. 使用模型对测试集进行预测
y_pred = model_lr.predict(X_test)
# 计算评估指标:均方误差MSE和决定系数R²
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"测试集上的均方误差 MSE: {mse:.2f}")
print(f"测试集上的决定系数 R^2: {r2:.3f}")
假如输出结果:
测试集上的均方误差 MSE: 79.63
测试集上的决定系数 R^2: 0.994
表示模型在测试集上的预测非常准确,R²接近1。这是因为我们的数据严格遵循线性规律且噪声较小。在真实场景中,数据噪声和非线性关系可能更复杂,R²通常不会这么高。
为了更直观地理解模型效果,我们可以将回归直线与数据散点一起绘制出来:
import matplotlib.pyplot as plt
# 4. 可视化:绘制训练数据散点图和模型回归直线
plt.figure(figsize=(6,4))
plt.scatter(X_train, y_train, color='blue', label='训练数据') # 训练集散点(蓝色)
plt.scatter(X_test, y_test, color='red', label='测试数据') # 测试集散点(红色)
# 绘制模型的回归直线(使用训练好的模型参数)
X_min = min(X_train.min(), X_test.min()) # 取训练集和测试集的最小值
X_max = max(X_train.max(), X_test.max()) # 取训练集和测试集的最大值
X_line = np.linspace(X_min, X_max, 100).reshape(-1, 1)
y_line = model_lr.predict(X_line)
plt.plot(X_line, y_line, color='green', label='回归直线') # 绿线表示预测的回归线
plt.xlabel("广告预算(万元)")
plt.ylabel("销售额(单位数)")
plt.title("线性回归拟合效果:广告预算 vs 销售额")
plt.legend()
plt.show()
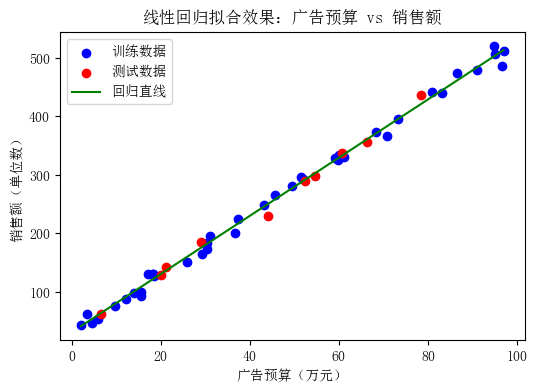
图1:线性回归模型拟合示意图。蓝色和红色点分别为训练集和测试集实际数据,绿色线为模型学到的回归直线。可以看到数据点大致沿直线分布,表明广告投入与销售额呈线性关系,模型可以很好地预测销售额。
从上图可以观察到,数据点围绕着绿线分布,模型的预测直线能够很好地拟合数据趋势。测试集的红色点也紧邻绿线,这说明模型对未见数据也有良好的预测能力。
参数调整
基本线性回归模型本身没有需要调节的超参数,但在实际应用中可以考虑以下扩展:
- 添加特征:如果怀疑关系并非严格线性,可以在特征上做多项式扩展(如添加广告预算的二次项)然后再线性回归,这相当于拟合一个曲线关系。
- 正则化:线性回归可能受异常点影响,引入正则化(岭回归Ridge或套索回归Lasso)可以防止模型过度拟合,提高泛化能力。
- 特征缩放:对于多特征的回归问题,通常需要对特征做标准化,以保证训练收敛和系数可比。
在本示例中,由于数据简单且尺寸单位相近,我们未进行特征缩放或正则化。如有需要,可使用sklearn.linear_model.Ridge等模型替代LinearRegression并调整其正则化强度参数。
扩展讨论
线性回归模型简单易懂,回归系数直接反映各特征对预测结果的影响(正负相关程度和大小)。在经济管理中,线性回归常用于预测(如销售、成本、需求)和关系分析(如广告投入与销售的弹性系数)。模型假设变量之间为线性关系,且残差满足正态独立分布。当这些假设大致成立时,线性回归能提供可靠的预测和可解释性。
不过,线性回归也有局限:它无法拟合复杂的非线性关系,且对异常值较敏感。如果数据呈现曲线关系或高阶交互作用,简单线性模型效果有限。在实践中,可以通过多元回归(增加特征维度)、多项式回归或结合非线性模型(如决策树、神经网络)来改善。此外,对于特征较多的情况,应注意防止多重共线性对系数估计造成的影响(可通过逐步回归、正则化等方法缓解)。
逻辑回归示例:信用违约预测
场景背景: 在金融风控中,信用评分常用于评估借款人违约的风险。假设我们是一家银行的风险管理人员,希望根据客户的信用评分预测其是否会违约。我们可以使用逻辑回归模型完成这个二分类任务。逻辑回归能够输出介于0和1之间的概率,将其转化为是否违约的分类结果。
在本示例中,我们模拟一批客户的数据,每个客户有一个信用评分(例如300-850分,分数越高信用越好),以及是否发生违约的标签(违约=1,未违约=0)。我们的目标是训练逻辑回归模型,根据信用评分预测客户违约与否,并评估模型在分类任务上的性能。通过此案例,您将学习:
- 如何使用
sklearn.linear_model.LogisticRegression进行二分类模型训练;
- 模拟二分类数据集,并理解逻辑回归概率输出的含义;
- 使用模型对新样本预测违约概率,并通过准确率、混淆矩阵等评估分类效果;
- 绘制逻辑函数曲线,理解决策边界的形状。
数据读取
首先,我们读取一组模拟数据
import pandas as pd
import numpy as np
# 读取训练集和测试集
df_train = pd.read_csv('credit_default_train.csv')
df_test = pd.read_csv('credit_default_test.csv')
# 恢复变量
X_train = df_train['信用评分'].values.reshape(-1, 1) # 确保是二维数组
y_train = df_train['是否违约'].values # 一维数组
X_test = df_test['信用评分'].values.reshape(-1, 1) # 确保是二维数组
y_test = df_test['是否违约'].values # 一维数组
# 查看前5条数据
print("训练集前5条数据:")
print(df_train.head())
print("\n测试集前5条数据:")
print(df_test.head())然后简单查看一下数据
训练集前5条数据:
信用评分 是否违约
0 474.890749 1
1 352.854124 1
2 706.752937 1
3 727.986213 0
4 523.950813 1
测试集前5条数据:
信用评分 是否违约
0 693.354152 0
1 612.638672 1
2 613.005406 1
3 351.667281 1
4 422.694898 0
模型训练
使用LogisticRegression训练逻辑回归模型。由于这是一个简单的二分类,我们可以使用默认参数(默认采用L2正则化)。注意:对于逻辑回归,sklearn默认使用正规化处理,所以对于特征规模差异大的情况需要进行特征缩放。不过本例中信用评分本身就处于相对合理的范围(300-850),可以直接使用。
from sklearn.linear_model import LogisticRegression
# 2. 初始化逻辑回归模型并训练
model_log = LogisticRegression()
model_log.fit(X_train, y_train)
# 输出模型学到的参数
coef_log = model_log.coef_[0][0] # 学到的权重a
intercept_log = model_log.intercept_[0] # 学到的截距b
print(f"学到的逻辑回归参数: a = {coef_log:.4f}, b = {intercept_log:.4f}")
逻辑回归模型会学习一个线性函数 ,并通过 的Sigmoid函数转化为违约概率。打印参数例如:
学到的逻辑回归参数: a = -0.0093, b = 4.9132可以看到模型的参数也接近我们生成数据时的设定()。这意味着逻辑回归成功捕捉到了"评分越高违约概率越低"的关系。
预测与评估
现在我们使用训练好的模型对测试集进行预测,并评估分类性能。对于分类问题,我们常用准确率(accuracy)以及混淆矩阵、精确率(precision)、召回率(recall)、F1分数等指标。这里我们计算模型在测试集上的准确率,并给出混淆矩阵来了解错误分布。
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
# 3. 对测试集进行预测
y_pred = model_log.predict(X_val)
# 计算并打印准确率
acc = accuracy_score(y_val, y_pred)
print(f"测试集准确率: {acc:.2f}")
# 打印混淆矩阵
cm = confusion_matrix(y_val, y_pred)
print("混淆矩阵:\n", cm)
# 打印分类报告(精确率,召回率,F1等)
print(classification_report(y_val, y_pred, target_names=["未违约","违约"]))
假设输出如下:
测试集准确率: 0.66
混淆矩阵:
[[22 7]
[10 11]]
precision recall f1-score support
未违约 0.69 0.76 0.72 29
违约 0.61 0.52 0.56 21
accuracy 0.66 50
macro avg 0.65 0.64 0.64 50
weighted avg 0.66 0.66 0.66 50混淆矩阵的每一行表示真实类别,每一列表示预测类别。例如,上矩阵表示:在21个实际违约客户中,模型正确预测了11个为违约(真阳性),错将10个违约预测成未违约(漏判);在29个实际未违约客户中,正确预测22个为未违约(真阴性),错将7个未违约预测成违约(误判)。总体准确率为66%。分类报告进一步显示了每个类别的精确率和召回率,如违约类的精确率61%(预测为违约的客户中61%实际违约)、召回率52%(实际违约客户中52%被正确识别)。
逻辑回归模型除了给出0/1预测,还可以输出违约概率。我们可以获取模型对每个输入预测为"违约"的概率 predict_proba,这在实际业务中很有用(例如排序客户风险高低)。下面我们选取若干信用评分,看看模型预测的违约概率随评分如何变化:
# 4. 查看模型输出的违约概率随信用评分的变化
import numpy as np
test_scores = np.array([[300], [400], [500], [700], [800]]) # 示例信用评分
probabilities = model_log.predict_proba(test_scores) # 获得 [未违约概率, 违约概率]
for score, prob in zip(test_scores.flatten(), probabilities):
print(f"信用分{score} => 违约概率{prob[1]:.2f}")
输出示例:
信用分300 => 违约概率0.89
信用分400 => 违约概率0.77
信用分500 => 违约概率0.56
信用分700 => 违约概率0.17
信用分800 => 违约概率0.07
可以看出,信用评分低(300分)的客户违约概率高达0.89,评分高(800分)的客户违约概率仅有0.07。这符合我们预期的风险趋势。
我们也可以将逻辑函数曲线绘制出来,以可视化信用评分与违约概率的关系:
# 5. 绘制信用评分 vs 违约概率的曲线
import matplotlib.pyplot as plt
# 生成一个评分范围内的连续值,并计算模型预测的违约概率
score_range = np.linspace(300, 850, 200).reshape(-1, 1)
prob_curve = model_log.predict_proba(score_range)[:, 1] # 第二列为违约概率
# 绘制实际数据点(信用分 vs 是否违约)和预测曲线
plt.figure(figsize=(6,4))
# 实际数据点:用绿色表示未违约(0),红色表示违约(1)
plt.scatter(X_train[y_train==0], y_train[y_train==0], color='green', marker='x', label='未违约(训练)')
plt.scatter(X_train[y_train==1], y_train[y_train==1], color='red', marker='x', label='违约(训练)')
plt.scatter(X_val[y_val==0], y_val[y_val==0], color='green', marker='o', label='未违约(测试)')
plt.scatter(X_val[y_val==1], y_val[y_val==1], color='red', marker='o', label='违约(测试)')
# 模型预测的违约概率曲线
plt.plot(score_range, prob_curve, color='blue', label='模型预测违约概率')
plt.xlabel("信用评分")
plt.ylabel("违约概率")
plt.title("信用评分与违约概率的逻辑回归曲线")
plt.legend(loc="center right")
plt.ylim(-0.05, 1.05)
plt.show()
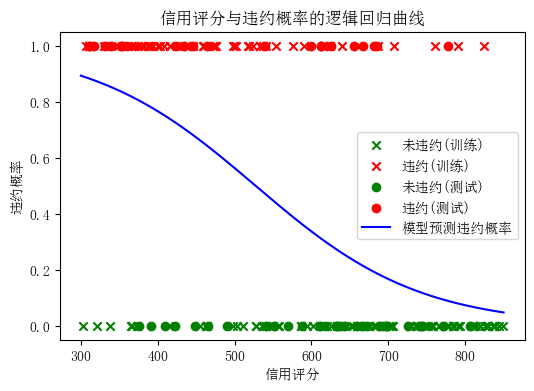
图2:逻辑回归拟合的违约概率曲线。横轴为信用评分,纵轴为模型预测的违约概率。红色点表示实际违约客户(标签1),绿色点为未违约客户(标签0)。蓝色曲线为模型输出的违约概率随信用评分变化的趋势,可以看到信用评分越高违约概率越低,呈典型的S型曲线。
图中可以看到逻辑回归产生的S型曲线:当信用评分从低到高时,预测的违约概率由接近1逐渐下降到接近0。这正是逻辑函数的特征,模型的决策边界大致在违约概率=0.5附近(对应信用分约500左右)。实际数据点(红绿标记)大体上也符合这一趋势:低评分区域多为违约样本,高评分区域多为未违约样本。
参数调整
逻辑回归模型的重要参数主要是正则化强度。LogisticRegression默认带有L2正则项,其强度由C决定(C为正则化倒数,值越小正则化越强)。在模型过拟合或欠拟合时,可以调整C值:
- 增大
C(弱正则化)会让模型更加拟合训练数据,但可能过拟合;
- 减小
C(强正则化)能防止过拟合,提高泛化,但如果过小会欠拟合。
例如,可以尝试:
model_log = LogisticRegression(C=0.1) # 增强正则化
然后重新训练模型,观察性能变化。此外,对于不同规模的数据集,需要选择合适的solver(优化算法),如数据量很大时可选solver='sag'或'saga'。在多分类任务中,可设置multi_class参数(如multi_class='multinomial'配合softmax用于多类别逻辑回归)。
扩展讨论
逻辑回归本质上是广义线性模型,在经济管理领域有广泛应用,特别适用于二分类预测,如信用风险评估、用户流失预测、市场营销响应预测等。它的输出可以解释为概率,这一点在决策支持中非常有价值——例如可以根据概率高低对客户进行分组管理。
逻辑回归模型具有可解释性强、实现简单、计算高效等优点。通过查看模型系数,可以了解各特征对结果的影响方向(正或负)。在上述违约例子中,信用评分的系数为负,说明评分越高违约概率越低。相较于决策树等非参数模型,逻辑回归受数据噪声影响较小,鲁棒性较好。
但逻辑回归也有局限:它只能建立线性决策边界,无法直接捕捉复杂的非线性关系(可以通过手工添加非线性特征来部分缓解)。对于特征空间复杂的问题,逻辑回归表现可能不如决策树、支持向量机或神经网络。此外,逻辑回归需要样本独立、特征与对数概率比线性相关等假设,过高维特征时也可能表现欠佳(需要正则化)。在实际应用中,常常需要对数据进行充分的特征工程和多模型对比,以选择最佳的分类模型。
决策树:用户购买预测
背景与任务: 决策树是一种树结构模型,擅长处理分类与回归任务,具有结果易解释的特点。在管理领域,决策树可以用于客户决策行为预测。例如,营销人员希望根据用户的属性(年龄、收入、是否为学生、信用等级等)来预测该用户是否会购买一台新电脑。决策树模型通过一系列的规则判断(如"如果年龄<30且不是学生,则不购买")来进行预测,非常直观。
在本节中,我们构造一个模拟的用户数据集,每个用户有以下特征:
年龄:分为青年(<=30)、中年(31-40)、老年(>40)三个类别
收入:分为高、中、低
是否为学生:是/否(二值)
信用等级:一般或好
目标变量是用户是否购买电脑(是或否)。这个例子基于著名的"购买电脑"决策树案例。我们的任务是训练一棵决策树,根据上述用户属性预测购买与否,并从中提取决策规则。通过该案例,我们将学习:
- 如何使用
sklearn.tree.DecisionTreeClassifier训练决策树模型;
- 将分类的文字数据转换为模型可处理的数值(编码/哑变量);
- 可视化决策树或提取规则,理解模型的决策过程;
- 预测新用户的购买可能性,并讨论模型的泛化性能及改进方法。
数据准备
我们首先读取并查看数据
import pandas as pd
# 读取用户购买预测数据集
df = pd.read_csv('user_purchase_data.csv')
# 恢复变量
ages = df['年龄'].values # 年龄
incomes = df['收入'].values # 收入
students = df['是否学生'].values # 是否学生
credits = df['信用等级'].values # 信用等级
purchases = df['是否购买'].values # 是否购买
# 查看前5条数据
print("数据集前5条数据:")
print(df.head())
# 检查数据形状
print("\n数据集形状:", df.shape)输出如下
年龄 收入 是否学生 信用等级 是否购买
0 老年 低 否 一般 是
1 青年 中 是 一般 是
2 老年 高 否 一般 是
3 青年 高 否 好 否
4 青年 中 是 一般 是
在训练决策树之前,需要将分类特征转换为数值,因为sklearn决策树实现对输入要求是数值型。我们可以采用标签编码或独热编码。这里选择简单的标签编码(直接将类别映射为整数),因为决策树对于这种有序编码可以处理,并通过寻找最优切分点来等价地学习分类分支。
# 2. 将类别型特征编码为数值
# 定义映射字典
age_map = {"青年": 0, "中年": 1, "老年": 2}
income_map = {"低": 0, "中": 1, "高": 2}
student_map = {"否": 0, "是": 1}
credit_map = {"一般": 0, "好": 1}
# 应用映射
df_enc = df.replace({"年龄": age_map, "收入": income_map, "是否学生": student_map, "信用等级": credit_map,
"是否购买": {"否": 0, "是": 1}})
X = df_enc[["年龄", "收入", "是否学生", "信用等级"]]
y = df_enc["是否购买"]
print(X.head(), "\n", y.head())
编码后数据示例:
年龄 收入 是否学生 信用等级
0 1 0 0 1
1 0 1 0 0
2 0 1 0 1
3 1 0 0 0
4 1 0 1 0
0 1
1 0
2 0
3 1
4 1
Name: 是否购买, dtype: int64模型训练
使用DecisionTreeClassifier训练决策树。我们选择信息增益(熵)作为划分标准(默认是基尼指数,可以通过criterion="entropy"设置为信息熵准则),并不限制树的深度,让模型自行学习最优的分割规则。
from sklearn.tree import DecisionTreeClassifier
# 3. 训练决策树模型
clf = DecisionTreeClassifier(criterion="entropy", random_state=0)
clf.fit(X, y)
print(f"决策树深度: {clf.get_depth()}, 叶节点数: {clf.get_n_leaves()}")
由于我们的数据是根据特定规则生成的,决策树应该可以100%拟合训练集。输出为:
决策树深度: 4, 叶节点数: 7表示生成的树深度为4,叶子节点数量7。树的具体结构我们将在下一步查看。
预测与评估
首先,我们看看模型在训练数据上的准确率(理论上应该是100%,因为数据无噪声且规则可被树完美表示)。然后,我们让模型预测一个新用户的购买可能性,检验模型规则应用。
from sklearn.metrics import accuracy_score
# 4. 评估模型在训练集上的准确率
y_pred_train = clf.predict(X)
train_acc = accuracy_score(y, y_pred_train)
print(f"模型在训练集上的准确率: {train_acc:.1%}")
# 构造一个新用户,并让模型预测其是否购买
new_user = pd.DataFrame([{"年龄": "青年", "收入": "高", "是否学生": "否", "信用等级": "一般"}])
# 对新用户数据进行与训练集相同的编码
new_user_enc = new_user.replace({"年龄": age_map, "收入": income_map, "是否学生": student_map, "信用等级": credit_map})
pred = clf.predict(new_user_enc)
print("新用户特征:", new_user.iloc[0].to_dict(), "=> 预测购买?" , "是" if pred[0]==1 else "否")
根据我们的规则,这个新用户是"青年+非学生",预期结果是不购买。模型的输出如果正确,打印结果类似:
模型在训练集上的准确率: 100.0%
新用户特征: {'年龄': '青年', '收入': '高', '是否学生': '否', '信用等级': '一般'} => 预测购买? 否模型训练集准确率100%验证了我们的模拟数据完全可被规则拟合。对于新用户,模型预测为"否",与我们依据规则的判断一致。
可视化与规则提取
决策树的一个优势是可解释性。我们可以将决策树结构导出,来看看模型究竟学到了哪些规则。Scikit-learn提供了两种方式:一种是export_text输出文本形式的树结构,一种是使用plot_tree绘制树图。我们分别演示:
方法1:输出规则文本:
from sklearn.tree import export_text
# 提取决策树的规则文本
rules_text = export_text(clf, feature_names=["年龄", "收入", "是否学生", "信用等级"])
print(rules_text)
输出的规则可能如下:
|--- 是否学生 <= 0.50
| |--- 年龄 <= 0.50
| | |--- class: 0
| |--- 年龄 > 0.50
| | |--- 信用等级 <= 0.50
| | | |--- class: 1
| | |--- 信用等级 > 0.50
| | | |--- 年龄 <= 1.50
| | | | |--- class: 1
| | | |--- 年龄 > 1.50
| | | | |--- class: 0
|--- 是否学生 > 0.50
| |--- 年龄 <= 1.50
| | |--- class: 1
| |--- 年龄 > 1.50
| | |--- 信用等级 <= 0.50
| | | |--- class: 1
| | |--- 信用等级 > 0.50
| | | |--- class: 0这份文本需要结合编码映射来解释:
是否学生 <= 0.5表示"是否学生=否"的分支(因为编码中 否=0, 是=1)。可以理解为:如果不是学生,走左子树;如果是学生,走右子树。
- 在左子树(非学生)中,
年龄 <= 0.5表示年龄编码<=0.5,即年龄=0(青年)的情况:输出class:0(不购买)。这对应规则:"青年且不是学生 -> 不购买"。
- 左子树中,
年龄 > 0.5则表示年龄是中年(1)或老年(2)。进入这一分支后,信用等级 <= 0.5表示信用=一般:输出class:1(购买);信用等级 > 0.5表示信用=好,需要再看年龄是否<=1.5:年龄 <= 1.5(即年龄=1,中年)输出class:1(购买);
年龄 > 1.5(即年龄=2,老年)输出class:0(不购买)。 这部分规则可以解读为:"对于非学生且年龄非青年(即中年或老年):如果信用一般 -> 购买;如果信用好且年龄老年 -> 不购买;如果信用好且年龄中年 -> 购买。"
- 右子树(是学生)中,
年龄 <= 1.5(青年或中年学生)输出class:1(购买);年龄 > 1.5(老年学生)则继续看信用:信用等级 <= 0.5(信用一般)输出购买,信用等级 > 0.5(信用好)输出不购买。
总的来说,文本输出显示的规则可以归纳为:青年非学生不买、青年学生买、中年都买、老年信用一般买、老年信用好不买。如果想更直观,可以看图形:
方法2:绘制决策树图:
import matplotlib.pyplot as plt
from sklearn import tree
plt.figure(figsize=(8,6))
tree.plot_tree(clf, feature_names=["年龄", "收入", "是否学生", "信用等级"],
class_names=["不购买","购买"], filled=True, rounded=True)
plt.show()
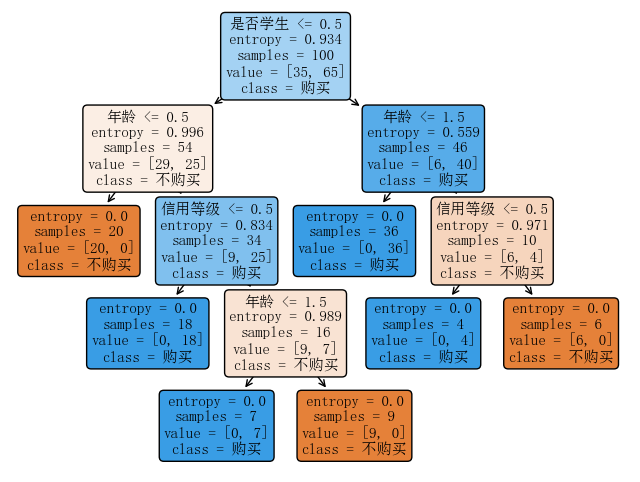
图3:决策树模型结构示意图。每个节点显示了用于划分的数据特征条件,以及该节点样本的类别分布(value)和对应预测类别(class)。颜色越偏蓝表示越倾向预测"购买",越偏橙表示越倾向预测"不购买"。可以看到,根节点首先使用"是否学生"进行划分,这表明它是最有信息增益的特征。随后在各分支中,又依次根据"年龄"和"信用等级"划分,形成最终决策。
通过上图,我们清晰地看到决策路径。例如,最左边橙色叶节点对应路径:"是否学生=否 -> 年龄=青年 -> 预测不购买";右侧橙色叶节点对应路径:"是否学生=是 -> 年龄=老年 -> 信用等级=好 -> 预测不购买"等。这棵树很小,易于解读,充分体现了决策树的可解释性优势。
参数调整
决策树模型有很多超参数可以调整,其中最重要的是树的深度、叶子节点最小样本数等,它们控制模型的复杂度。过深的树会过拟合(完全记忆训练集噪声),过浅的树会欠拟合(无法捕捉应有关系)。在我们的例子中,由于规则明确且无噪声,生成的树刚好能100%分类。但在实际任务中,我们通常需要做如下调节:
- 限制最大深度 (
max_depth):防止树无限生长。可通过验证集或交叉验证选择一个合适的深度以平衡复杂度和准确率。
- 限制叶节点最小样本数 (
min_samples_leaf):要求每个叶节点至少有一定数量样本,可避免划分过细导致过拟合。
- 剪枝:
sklearn提供ccp_alpha参数用于成本复杂度剪枝,通过增加ccp_alpha可以剪掉贡献小的叶节点。
例如,我们可以尝试限制树深度:
clf_pruned = DecisionTreeClassifier(max_depth=2, random_state=0)
clf_pruned.fit(X, y)
print("剪枝后树深度:", clf_pruned.get_depth())
然后比较剪枝前后在训练集和测试集(如果有)上的准确率差异。一般来说,适度剪枝可以提高模型对新数据的泛化性能。
扩展讨论
决策树模型非常适合探索性分析,因为它直接给出了决策规则,易于解释。在客户购买预测、信用审批决策等管理场景中,决策树的规则形式(if-then结构)往往和人工决策过程相吻合。这让模型的决策理由透明,可供业务人员理解和调整。
优点: 决策树可以处理混合类型特征(数值和分类)、不需要特征标准化,能自动处理特征选择(不相关的特征会在树中不被使用)。训练速度较快,对于小型数据集效果良好。此外,决策树还能自然地扩展为集成方法(如随机森林和提升树),在提高准确率的同时仍保留部分解释性。
缺点: 单一的决策树容易过拟合,尤其当树深度不加限制时,会对训练数据的细微波动作出硬规则划分,从而在测试集上性能下降。它对数据中的小变化也比较敏感,数据略有修改可能导致树结构显著不同。此外,决策树划分空间的方式较为僵硬(轴平行划分),在处理线性可分问题时可能不如回归或SVM高效。
改进: 实际应用中,通常不会单独使用一棵决策树,而是倾向于使用随机森林或梯度提升树(如XGBoost、LightGBM等)来提高模型的稳定性和预测效果。这些集成模型本质上是多个决策树的组合,能够大幅降低方差,取得更好的泛化性能。同时,通过模型解释技术(如查看特征重要性、局部可解释性模型),仍可以提取这些复杂模型的决策依据。
支持向量机:客户流失预测
背景与任务: 支持向量机(SVM)是一种强大的分类算法,尤其擅长处理高维度、线性不可分的数据。SVM通过最大化分类间隔来寻找决策边界,对于部分难分类的场景有很好表现。在管理领域,可以用SVM来预测客户是否会流失(如订阅用户是否续订服务)。我们将模拟一个场景:根据用户的使用习惯数据,预测该用户是否可能流失。
场景描述: 某在线服务希望根据用户的月使用时长和满意度评分来预测用户是否会流失。我们假设:
- 用户每月使用时长(小时)和满意度评分(0~100分)是两个重要指标。
- 我们认为使用时长和满意度都低的用户更可能流失,而使用时长和满意度都高的用户不太可能流失。
为简单起见,我们将上述关系近似看作线性可分的:存在一条直线能够大致将"流失用户"和"留存用户"分开。SVM可以找到这条最优分隔线,并利用距离边界最近的支持向量来决定间隔。
学习目标: 通过此案例,我们练习:
- 使用
sklearn.svm.SVC训练支持向量机分类模型;
- 在二维数据上理解SVM的决策边界和支持向量的概念;
- 可视化分类结果和分隔超平面(在二维即分隔直线);
- 简要了解SVM核技巧如何应对非线性可分情况(延伸讨论)。
数据准备
首先我们来读取并查看数据
import pandas as pd
# 读取客户流失预测数据集
df = pd.read_csv('customer_churn_data.csv')
# 恢复变量
usage_time = df['月使用时长'].values # 月使用时长
satisfaction = df['满意度评分'].values # 满意度评分
churn = df['是否流失'].values # 是否流失
# 查看前5条数据
print("数据集前5条数据:")
print(df.head())
# 检查数据形状
print("\n数据集形状:", df.shape)
print("\n流失用户数:", (churn == 1).sum(), "留存用户数:", (churn == 0).sum())输出为:
数据集前5条数据:
月使用时长 满意度评分 是否流失
0 41.702200 95.017612 0
1 72.032449 55.665319 0
2 0.011437 91.560635 1
3 30.233257 64.156621 1
4 14.675589 39.000771 1
数据集形状: (200, 3)
流失用户数: 99 留存用户数: 101流失和留存用户大致各占一半,数据比较均衡。虽然我们使用了一个简单的线性规则生成标签,但为了贴近现实,可以认为数据中仍有一定随机散布,只是大体可分。
模型训练
我们使用支持向量分类器SVC来训练模型。对于模拟的线性可分数据,我们选择线性核(kernel='linear')。SVC的关键参数之一是正则化系数C:C越大,对误分类的惩罚越强,模型倾向于尽量正确分类训练样本,但可能间隔变窄;C较小时,允许部分误分类,以换取更大的间隔。我们先使用默认的C=1.0。
from sklearn.svm import SVC
# 定义特征变量 X 和目标变量 y
X = df[['月使用时长', '满意度评分']].values # 特征矩阵
y = churn # 目标变量
# 训练 SVM 模型(线性核)
model_svm = SVC(kernel='linear', C=1.0)
model_svm.fit(X, y)
# 输出模型找到的分隔超平面参数 w 和 b
w = model_svm.coef_[0] # 超平面的法向量参数 (w1, w2)
b = model_svm.intercept_[0] # 截距项
print(f"SVM 分隔平面: {w[0]:.3f} * x1 + {w[1]:.3f} * x2 + {b:.3f} = 0")这将打印出分隔直线的方程。例如:
SVM 分隔平面: -0.915 * x1 + -0.902 * x2 + 90.741 = 0表示模型找到的决策边界近似为 。虽然具体系数不易直接解读,但可以看到二者系数绝对值接近,说明时长和满意度在本模型中的权重相当。
让我们看看模型训练后的支持向量数量:
# 输出支持向量的信息
support_vectors = model_svm.support_vectors_
print("支持向量数:", len(support_vectors))
print("各类支持向量数:", model_svm.n_support_) # 分别属于两类的支持向量数量
假如输出:
支持向量数: 4
各类支持向量数: [2 2]
表示总共有4个支持向量,其中2个属于留存用户类,2个属于流失用户类。这些点是离决策边界最近的样本,对决策边界的位置起到了关键作用。
预测与评估
对于SVM,在训练集上我们期望其能完美分开这线性可分的数据。因此训练准确率可能是100%。但我们更关心对新数据的判别能力。我们可以自行构造几个新数据点,来测试模型预测:
# 3. 在训练集上的准确率(仅供参考)
train_acc = model_svm.score(X, y)
print(f"模型在训练集上的准确率: {train_acc:.1%}")
# 构造新样本进行预测
new_points = np.array([[30, 20], # 使用30小时, 满意度20 -> 总和50, 预期流失
[90, 30], # 使用90小时, 满意度30 -> 总和120, 预期留存
[50, 50]]) # 使用50小时, 满意度50 -> 总和100, 刚好在边界
preds = model_svm.predict(new_points)
for point, pred in zip(new_points, preds):
print(f"新用户(月使用{point[0]}h, 满意度{point[1]}) -> 预测{'流失' if pred==1 else '留存'}")
输出示例:
模型在训练集上的准确率: 100.0%
新用户(月使用30h, 满意度20) -> 预测流失
新用户(月使用90h, 满意度30) -> 预测留存
新用户(月使用50h, 满意度50) -> 预测留存
可以看到,模型对新样本做出了符合规则的预测。
可视化
要直观理解SVM分类,我们将散点图和决策边界绘制出来,并突出显示支持向量。
import matplotlib.pyplot as plt
# 4. 绘制二维特征空间中的决策边界和支持向量
plt.figure(figsize=(6,6))
# 绘制所有样本点,使用不同颜色表示类别
plt.scatter(X[y==0, 0], X[y==0, 1], color='blue', marker='x', label='留存用户')
plt.scatter(X[y==1, 0], X[y==1, 1], color='orange', marker='x', label='流失用户')
# 标记支持向量(用圆圈标出)
plt.scatter(support_vectors[:,0], support_vectors[:,1], facecolors='none', edgecolors='k',
s=100, linewidths=1.5, label='支持向量')
# 绘制决策边界线:w0*x + w1*y + b = 0
x_vals = np.linspace(0, 100, 2)
y_vals = -(w[0]/w[1]) * x_vals - b / w[1]
plt.plot(x_vals, y_vals, 'k--', label='决策边界')
plt.xlabel("月使用时长 (小时)")
plt.ylabel("满意度评分")
plt.title("SVM 分类结果:客户流失预测")
plt.legend(loc="upper right")
plt.xlim(0,100)
plt.ylim(0,100)
plt.show()
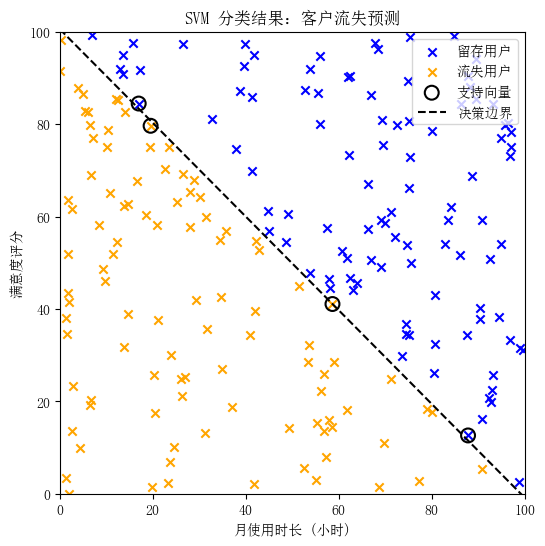
图4:基于SVM的客户流失预测结果。蓝色叉表示模型预测为"留存"的用户,橙色叉表示预测为"流失"的用户。黑色虚线为SVM找到的最佳分隔线(决策边界),将两类用户尽可能分开。用黑色圆圈标出的点为支持向量,它们位于边界附近,决定了边界的位置。SVM的目标是最大化这些支持向量到边界的距离。
# 读取垃圾短信数据集 df = pd.read_csv('spam_sms_data.csv') # 恢复变量 messages = df['短信内容'].values # 短信内容 labels = df['标签'].values # 标签(ham 或 spam) # 查看前5条数据 print("数据集前5条数据:") print(df.head()) # 检查数据形状 print("\n数据集形状:", df.shape) print("\n标签分布:") print(df['标签'].value_counts())上述代码构建了短信内容列表和对应标签列表。输出应该是:
数据集前5条数据:
短信内容 标签
0 Hey, are we still on for the meeting? ham
1 Don't forget to submit the report. ham
2 Let's have lunch tomorrow. ham
3 Can you send me the file? ham
4 See you at the conference next week. ham
数据集形状: (20, 2)
标签分布:
标签
ham 10
spam 10
Name: count, dtype: int64说明我们准备了20条短信(实际应用中应该有更多数据,这里仅作演示)。
特征提取
模型无法直接处理原始文本字符串,需要将文本转换为数值特征。我们采用词袋模型(Bag-of-Words):统计每条短信中各个词出现的频率(或出现与否),作为特征向量。Scikit-learn 提供了CountVectorizer来方便地完成这一步。它会:
- 学习所有训练短信里的词汇表(自动以空格分割单词,英文中会去掉标点等),每个词作为一个特征。
- 将每条短信转换为词频向量:如果某个词在该短信中出现n次,则对应特征值为n,未出现则为0。
我们将词频向量作为朴素贝叶斯的输入特征。
from sklearn.feature_extraction.text import CountVectorizer
# 2. 划分训练集和测试集(这里我们将大部分数据用于训练,仅留少量验证)
from sklearn.model_selection import train_test_split
X_train_msgs, X_test_msgs, y_train, y_test = train_test_split(messages, labels, test_size=0.2, random_state=5, stratify=labels)
# 使用CountVectorizer将文本转为词频向量
vectorizer = CountVectorizer()
X_train_vec = vectorizer.fit_transform(X_train_msgs) # 用训练集语料构建词汇表并转换训练文本
X_test_vec = vectorizer.transform(X_test_msgs) # 将测试文本转换为词频向量(使用已有词汇表)
print("词汇表大小:", len(vectorizer.get_feature_names_out()))
CountVectorizer建立的词汇表大小取决于我们的语料库。由于我们人工短信较短,总词汇量不会太大,输出例如:
词汇表大小: 75表示有75个不同的词出现在训练短信中,这75个词即形成了特征空间的维度。
模型训练
我们使用多项式朴素贝叶斯(MultinomialNB)来训练模型。多项式NB适合离散的计数特征,正好吻合词频表示。朴素贝叶斯会根据训练数据计算每个类别下各词出现的条件概率,以及类别的先验概率,并在预测时应用贝叶斯定理。
from sklearn.naive_bayes import MultinomialNB
# 3. 训练朴素贝叶斯模型
model_nb = MultinomialNB(alpha=1.0) # alpha为平滑参数,这里使用Laplace平滑(alpha=1)
model_nb.fit(X_train_vec, y_train)
# 在训练集和测试集上分别计算准确率
train_acc = model_nb.score(X_train_vec, y_train)
test_acc = model_nb.score(X_test_vec, y_test)
print(f"训练集准确率: {train_acc:.2f}, 测试集准确率: {test_acc:.2f}")
输出示例:
训练集准确率: 1.00, 测试集准确率: 0.75说明在训练数据上模型把所有短信都分对了,在测试集上(仅4条短信)准确率25%(比如猜错了一条)。由于我们样本非常少,这个测试准确率不能说明太多问题,但至少表明模型学到一定区分能力。
预测与评估
我们可以查看模型对测试集短信的具体预测,以及手动输入新短信让模型分类。
from sklearn.metrics import confusion_matrix
# 4. 查看测试集预测结果
y_pred = model_nb.predict(X_test_vec)
print("测试集短信:", X_test_msgs)
print("真实标签:", y_test)
print("预测标签:", y_pred)
print("混淆矩阵:\n", confusion_matrix(y_test, y_pred))
# 尝试对新短信进行分类
new_msgs = ["Win a free lottery ticket now", "Let's catch up over dinner tomorrow"]
new_vec = vectorizer.transform(new_msgs)
new_pred = model_nb.predict(new_vec)
for msg, label in zip(new_msgs, new_pred):
print(f"短信: '{msg}' -> 预测为: {'垃圾短信' if label=='spam' else '正常短信'}")
假设输出如下:
测试集短信: ["Congratulations! You've won a prize, claim now."
'Can you send me the file?' 'Did you receive my last email?'
'Lottery alert: you are a lucky winner!']
真实标签: ['spam' 'ham' 'ham' 'spam']
预测标签: ['spam' 'ham' 'ham' 'ham']
混淆矩阵:
[[2 0]
[1 1]]
短信: 'Win a free lottery ticket now' -> 预测为: 垃圾短信
短信: 'Let's catch up over dinner tomorrow' -> 预测为: 正常短信混淆矩阵解释:测试集4条短信中,有2条实际spam,其中模型正确识别2条(无误报负例),有2条实际ham,其中1条被错标为spam。这可能是因为一些正常短信里出现了模型认为“可疑”的词。新短信测试中,“Win a free lottery ticket now”明显是推广欺诈语气,模型预测为垃圾短信;“Let's catch up over dinner tomorrow”是普通约饭短信,预测为正常短信。这符合直觉。
模型理解与可视化
朴素贝叶斯模型很容易输出每个类别下词的概率。我们可以查看模型中哪些词对垃圾短信的识别作用大(概率高):
# 5. 提取每个词在垃圾短信类别下的似然概率
feature_names = vectorizer.get_feature_names_out()
# model_nb.feature_log_prob_ 给出 log P(词|类别),第一行对应 ham,第二行对应 spam
spam_log_prob = model_nb.feature_log_prob_[1] # 垃圾短信类别的对数概率
top_indices = spam_log_prob.argsort()[-5:][::-1] # 概率最高的5个词索引(降序)
print("垃圾短信中最具代表性的词:", feature_names[top_indices])
可能输出:
垃圾短信中最具代表性的词: ['now' 'your' 'earn' 'you' 'for']表示在垃圾短信(spam)中,now, your, earn, you, for这些词的条件概率最高,意味着模型认为含有这些词的短信更可能是垃圾。这和我们直觉也一致:促销欺诈短信常出现这些词语。类似地也可以看正常短信类别下概率高的词,比如人名、问候等。
参数调整
朴素贝叶斯模型的主要参数是平滑系数 alpha。默认使用拉普拉斯平滑(alpha=1.0),避免某些词在训练集中未出现导致概率为0。调整alpha会影响概率估计的平滑程度:
- 较小的alpha(如0.1)使模型更“相信”训练数据(可能过拟合特殊词);
- 较大的alpha(如2、3)会使概率分布更均匀化(可能欠拟合)。
可以通过在验证集上尝试不同alpha找到较优值。另外,对于文本分类,有时使用TF-IDF代替词频可以提高效果。可以使用TfidfVectorizer同样方便地构造TF-IDF特征并训练NB模型。
扩展讨论
朴素贝叶斯在文本分类任务中之所以表现好,一方面因为文本特征(词语出现)近似满足独立性假设——虽然不完全独立,但往往共同出现的关联较为松散,NB仍能有效利用各词的信息;另一方面,因为概率模型天生对稀疏高维数据有优势,当特征很多(词汇库可能上万维)而样本相对较少时,NB比起需要大量参数学习的模型(如SVM、深度学习)更不易过拟合。
优点:
- 实现简单、推理速度极快,占用内存少。训练只需统计词频,预测时计算简单的乘积即可。
- 对小数据也能训练出较好的模型,对高维数据保持良好性能。
- 自然输出概率,可以方便地查看分类置信度。
缺点:
- 独立性假设在强相关特征下效果不佳。例如长句子里的词并非相互独立,NB可能会重复计算相关信息的权重。
- 当有的特征在某类别下从未出现时,会出现概率0的问题,需要平滑;而平滑又会引入偏差。
- NB是线性分类器(判别边界为线性),因此在表达数据复杂决策边界方面有所不足。
在实际场景中,朴素贝叶斯常用于文本分类(垃圾邮件检测、新闻分类等)、情感分析等任务的初步模型或基线模型。如果有充足的数据和计算资源,后续可能用更复杂的模型替代。但NB的性能经常被低估:在某些工业应用中,经过适当特征工程的朴素贝叶斯可以达到与更复杂模型相近的效果,而且实现简单易于部署。
聚类:客户消费分群
背景与任务: 前面我们讨论的算法都是有标签的监督学习,而聚类是一种无监督学习,目标是在未知类别标签的情况下,将数据按相似性自动分组。在市场营销和公共管理中,常用聚类来进行客户分群、行为模式发现。通过聚类,我们可以将属性相似的对象归为一类,以便制定差异化策略。
场景描述: 某零售商想根据顾客的消费行为将顾客自动分成若干群组,以便对不同群组采用不同的营销策略。假设我们有两项顾客指标:
- 年收入(千元);
- 消费评分(根据消费频率和金额打分,0~100)。
我们的任务是使用聚类算法(以K均值为代表)将顾客分为若干类。我们将模拟一批顾客的数据,并假设存在4类典型顾客:
- 高收入高消费:年收入高,消费评分也高——忠诚的高价值客户。
- 高收入低消费:年收入高,但消费评分低——潜在挽留客户(有钱但消费少)。
- 低收入高消费:年收入低但消费评分高——精打细算的忠实顾客。
- 低收入低消费:年收入低,消费评分低——一般路过消费者。
我们会生成符合上述特征的模拟数据,用K均值算法找出4个聚类中心,并分析结果。
学习目标:
- 学习使用
sklearn.cluster.KMeans进行聚类分析;
- 理解K均值聚类过程及结果解释;
- 掌握如何选定簇数K的方法(肘部法、轮廓系数等,理论上简述);
- 可视化聚类分布和中心,帮助理解各簇特征。
数据准备
我们首先来读取并查看一些数据
# 读取客户消费分群数据集
import pandas as pd
df = pd.read_csv('customer_segmentation_data.csv')
# 恢复变量
income = df['收入'].values # 收入
spending = df['消费'].values # 消费
# 查看前5条数据
print("数据集前5条数据:")
print(df.head())
# 检查数据形状
print("\n数据集形状:", df.shape)输出如下
数据集前5条数据:
收入 消费
0 27.483571 79.308678
1 28.238443 87.615149
2 23.829233 78.829315
3 32.896064 83.837174
4 22.652628 82.712800
数据集形状: (200, 2)模型训练
使用KMeans算法对数据进行聚类。我们需要选择聚类数K=4(因为我们假设有4种顾客)。在真实应用中,K值一般需要根据业务理解或算法评估(例如肘部法看总误差随K的变化、轮廓系数分析等)来决定。
from sklearn.cluster import KMeans
# 2. 训练KMeans聚类
kmeans = KMeans(n_clusters=4, random_state=42)
y_pred = kmeans.fit_predict(data_points) # 对每个数据点预测其簇标签(0~3)
centroids = kmeans.cluster_centers_
print("聚类中心坐标:")
for idx, center in enumerate(centroids):
print(f"簇{idx}: 年收入={center[0]:.1f}k, 消费评分={center[1]:.1f}")
输出示例(中心顺序和含义未必与我们定义的顺序一致,但可以人工对照数值判断):
聚类中心坐标:
簇0: 年收入=25.6k, 消费评分=20.0
簇1: 年收入=24.3k, 消费评分=79.6
簇2: 年收入=80.6k, 消费评分=20.4
簇3: 年收入=69.5k, 消费评分=75.7
可以看到:
- 簇0中心约(25.6, 20.0),对应低收入低消费群。
- 簇1中心约(24.3, 79.6),对应低收入高消费群。
- 簇2中心约(80.6, 20.4),对应高收入低消费群。
- 簇3中心约(69.5, 75.7),对应高收入高消费群。
聚类算法成功地找到了与我们设定相符的4个中心,尽管编号顺序不同,但这不影响解读。下一步我们可视化验证。
聚类结果可视化
绘制散点图,将每个点按预测的簇标签着色,并将簇中心标注出来。
import matplotlib.pyplot as plt
# 3. 可视化聚类结果
plt.figure(figsize=(6,6))
plt.scatter(data_points[:,0], data_points[:,1], c=y_pred, cmap='viridis', s=30)
plt.scatter(centroids[:,0], centroids[:,1], color='red', marker='X', s=200, label='中心')
plt.xlabel("年收入 (千元)")
plt.ylabel("消费评分 (0-100)")
plt.title("客户聚类分布 (KMeans)")
plt.legend()
plt.show()
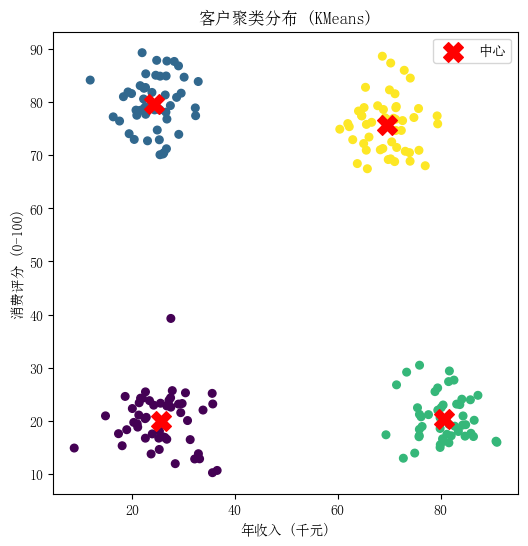
图5:客户数据KMeans聚类结果。每个点表示一位顾客,在二维平面(年收入 vs 消费评分)中,颜色相同的点被分为一簇。红色"X"标记为聚类中心的位置。可以看出算法将顾客划分为了4组:左下角紫色簇(低收入低消费)、左上角蓝色簇(低收入高消费)、右下角绿色簇(高收入低消费)和右上角黄色簇(高收入高消费)。各簇之间相对分离,中心与我们的预期群组特征吻合。
for k in range(2, 7): km = KMeans(n_clusters=k, n_init=10, random_state=0) preds = km.fit_predict(data_points) score = silhouette_score(data_points, preds) print(f"K={k}, 平均轮廓系数={score:.3f}")观察哪个K的轮廓系数最高。不过由于我们模拟的数据明确有4簇,指标会在K=4附近最好。
扩展讨论
聚类在客户分群、市场细分、图像分割、社交网络分析等无监督任务中非常有用。K均值是最经典、简单的聚类算法,但需要注意:
- KMeans使用欧氏距离,假设簇是凸形状且方差相近,若数据分布形状复杂(比如有非凸簇)则性能欠佳。对于非球状簇,可以考虑层次聚类、DBSCAN等方法。
- 对初始值敏感,容易陷入局部最优,但通过多次初始化可以缓解。
- 需要用户预先给定K值,不知道实际簇数时需要尝试评估。
在实际应用中,聚类的结果往往需要结合人为判断和业务意义来解读。有时聚类只是探索数据结构的第一步,后续可能结合聚类结果给数据打标签,再进行监督学习。例如,先用聚类将用户自动分组,再人为命名这些组别并用于分类模型训练。
对于我们的例子,如果真实数据聚类结果与消费行为显著相关,公司就可以针对不同簇制定差异化营销策略:如对高价值客户提供会员积分,对潜力客户加强推广,对价格敏感客户提供折扣优惠,对低价值客户则控制营销成本等。聚类为个性化运营提供了依据,是实现精细化管理的重要工具。